Lyrebird_Cycles
Well-Known Member
- Joined
- 10/7/16
- Messages
- 1,439
- Reaction score
- 777
As has been well documented, refractometers and densitometers give different results in wort and beer, reflected in multiple sources giving calculations for correction factors for refractometers. This first post will delve into the background of why the discrepancies exist. A follow up will give some data on a better approach to correction factors than the ones commonly used, but still imperfect. This is a work in progress, more data is needed before we can get to a definitive approach.
The density of a solution is determined by the way the molecules pack together which depends on the partial molar volumes of the solutes and solvent and the electrostatic interactions between them. In the case of sugar solutions in water there is very little difference between the ratios of partial molar volume to molecular weight for different sugars so their density / concentration functions are also very similar. For more than you could ever want to know on this see: http://www.ub.uib.no/elpub/2001/h/415001/Hovedoppgave.pdf
A consequence of this is that wt% solutions of glucose, sucrose and maltose as functions of density are almost identical in the ranges in which we are interested.
Refractive index, however, does change between different sugars.
Why?
Refractive index is the ratio of the speed of light in a vacuum to the speed of light in a material. The explanation of why the speed of light changes in different materials involves some fundamental physics: the speed of light in a material is dependent on the square root of the dielectric constant of the material, which in turn is the product of the electric permittivity and the magnetic permeability. Fortunately for us the magnetic permeability of most materials at light wavelengths equals 1 (ferromagnetic materials being the obvious exception). This means we only have to worry about the electric permittivity, which depends on polarisable dipoles: any pair of charged particles separated in space are a dipole, so all materials have plenty of them. These dipoles are excited by the incoming electric field and respond by vibrating at the same frequency but 90 degrees out of phase, with the response wave behind the excitation wave. This causes a net slowing in the speed of light in the material (phase delay).
This means that the number and polarizability of the dipoles determines the net speed of light (Lorentz- Lorenz relation). The number of dipoles per unit volume increases with density, so for a given material the speed of light is inversely proportional to square root of density and refractive index follows this same relationship. Different materials have different dipole arrangements, this changes the mean polarizability which in turn changes the relationship between refractive index and density.
This applies to sugars: different sugars, even when they are isomers of one another, have different dipole arrangements so the relationship between refractive index and density will also change.
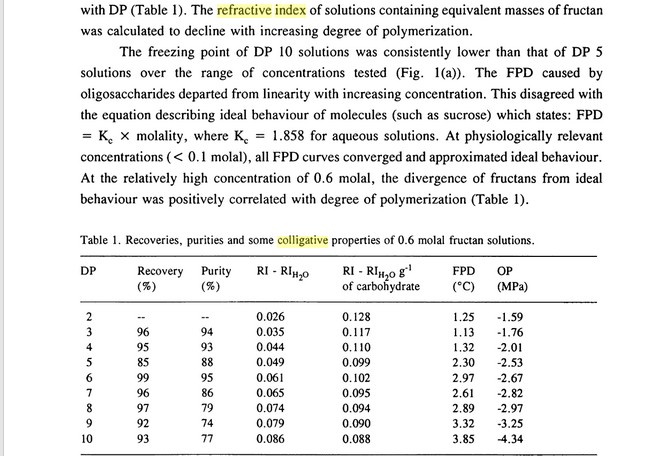
Another factor that affects the relationship between refractive index and density is the degree of polymerisation* of the sugar: as the degree of polymerisation increases, the ratio of refractive index to density decreases. The reason for this goes back to the Lorentz Lorenz relation, which depends on the number of molecules per unit volume. This logically decreases with increasing polymerisation (assuming constant density).
Practical refractometers work by using total internal reflection to determine the ratio between the refractive index of the sample and the refractive index of a transparent solid, usually quartz in cheap models and aluminium oxide (sapphire) in better ones.
Assuming you are still following this, we now have the theoretical basis on which we can construct a rational interpretation of the available empirical data.
That will be tomorrow.
* Degree of polymerisation (DP) is a shorthand for the number of hexose moieties per molecule eg glucose DP = 1, sucrose and maltose DP =2, maltotriose DP = 3, maltotetrose DP = 4. For dextrins, another method of expressing this is the dextrose equivalence (DE), the two are related:
DP x DE = 120. The degree of polymerisation of malt derived dextrins varies with the mash profile, a mean degree of polymerisation of 6-8 appears to be typical of the maltodextrin fraction in ordinary worts.
The density of a solution is determined by the way the molecules pack together which depends on the partial molar volumes of the solutes and solvent and the electrostatic interactions between them. In the case of sugar solutions in water there is very little difference between the ratios of partial molar volume to molecular weight for different sugars so their density / concentration functions are also very similar. For more than you could ever want to know on this see: http://www.ub.uib.no/elpub/2001/h/415001/Hovedoppgave.pdf
A consequence of this is that wt% solutions of glucose, sucrose and maltose as functions of density are almost identical in the ranges in which we are interested.
Refractive index, however, does change between different sugars.
Why?
Refractive index is the ratio of the speed of light in a vacuum to the speed of light in a material. The explanation of why the speed of light changes in different materials involves some fundamental physics: the speed of light in a material is dependent on the square root of the dielectric constant of the material, which in turn is the product of the electric permittivity and the magnetic permeability. Fortunately for us the magnetic permeability of most materials at light wavelengths equals 1 (ferromagnetic materials being the obvious exception). This means we only have to worry about the electric permittivity, which depends on polarisable dipoles: any pair of charged particles separated in space are a dipole, so all materials have plenty of them. These dipoles are excited by the incoming electric field and respond by vibrating at the same frequency but 90 degrees out of phase, with the response wave behind the excitation wave. This causes a net slowing in the speed of light in the material (phase delay).
This means that the number and polarizability of the dipoles determines the net speed of light (Lorentz- Lorenz relation). The number of dipoles per unit volume increases with density, so for a given material the speed of light is inversely proportional to square root of density and refractive index follows this same relationship. Different materials have different dipole arrangements, this changes the mean polarizability which in turn changes the relationship between refractive index and density.
This applies to sugars: different sugars, even when they are isomers of one another, have different dipole arrangements so the relationship between refractive index and density will also change.
Another factor that affects the relationship between refractive index and density is the degree of polymerisation* of the sugar: as the degree of polymerisation increases, the ratio of refractive index to density decreases. The reason for this goes back to the Lorentz Lorenz relation, which depends on the number of molecules per unit volume. This logically decreases with increasing polymerisation (assuming constant density).
Practical refractometers work by using total internal reflection to determine the ratio between the refractive index of the sample and the refractive index of a transparent solid, usually quartz in cheap models and aluminium oxide (sapphire) in better ones.
Assuming you are still following this, we now have the theoretical basis on which we can construct a rational interpretation of the available empirical data.
That will be tomorrow.
* Degree of polymerisation (DP) is a shorthand for the number of hexose moieties per molecule eg glucose DP = 1, sucrose and maltose DP =2, maltotriose DP = 3, maltotetrose DP = 4. For dextrins, another method of expressing this is the dextrose equivalence (DE), the two are related:
DP x DE = 120. The degree of polymerisation of malt derived dextrins varies with the mash profile, a mean degree of polymerisation of 6-8 appears to be typical of the maltodextrin fraction in ordinary worts.